베주 항등식 (Bezout's Identity)
두 정수의 최대공약수를 원래 두 수의 배수의 합으로 나타낼 수 있다.

이때 x 와 y 는 베주 계수(Bezout coefficient)라고 한다!!
정리하자면 GCD(a, b) = d라고 할 때,
- ax + by = d를 만족하는 정수 x, y가 존재한다
- d는 정수 x, y에 대해서 ax + by로 표현할 수 있는 가장 작은 정수이다.
- ax + by로 표현될 수 있는 모든 정수는 d의 배수이다.
확장 유클리드 호제법(Extended Euclidean algorithm)
위와 같은 베주 항등식과 비슷하게 확장 유클리드 호제법은
ax + by = d 라고 할때, d = GCD(a, b)에 대하여 (x, y)의 값을 찾는 효율적인 알고리즘이다!!
나중에 RSA를 복호화할때 e값의 modular inverse를 구하기 위해 이 알고리즘을 사용해야함!

-> 쉽게 쓰자면,, gcd(a, b)의 값을 어떤 방정식으로 표현하고 그 계수(x, y)를 찾는 과정!!
사실 확장 유클리디안 호제법을 쓰면 modular inverse도 쉽게 구할 수 있다.
modular inverse란?
x*y = 1 (mod n) 일때, y는 x의 mod n inverse -> y = x^(-1) 이라고도 표현함

ex)
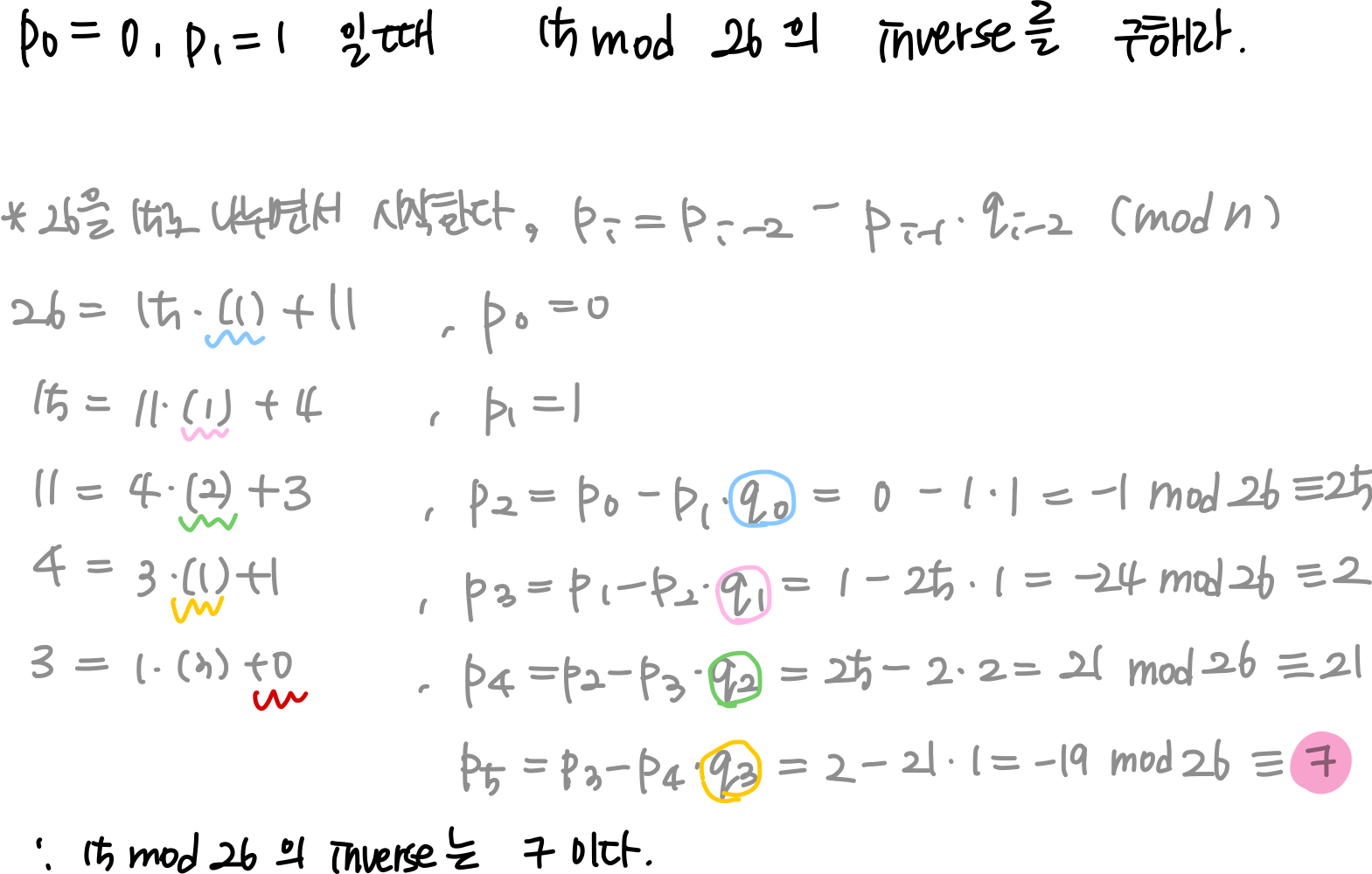
퀴즈)
p = 26513, q = 32321 일때,
p*u + q*v = gcd(p,q)를 만족하는 u, v를 구해라. (이때, u, v 중 더 작은 숫자가 플래그값)

함수의 작동원리를 알아봅쉬다
1. b가 0이면, a자체가 최대공약수이므로 (a, 1, 0)을 반환
2. 그렇지 않으면, b와 a % b에 대해 함수를 재귀적으로 호출하고, 결과를 이용하여 최대공약수 및 u, v (베주 항) 계산
gcd, u, v = extended_gcd(b, a % b)-> 이때! 재귀 호출을 통해 b가 0이 될때까지 계속 하위단계로 진행!!
a%b를 하는 이유는 유클리드 알고리즘 때문에~ (a, b의 최대공약수는 b, a%b의 최대공약수와 같음)
return gcd, v, u - (a // b) * v이때 재귀 호출을 통해서 새로운 값으로 업데이트를 해야하는데

요런식으로!!
그래서 a//b는 a를 b로 나눈 몫이고, 이게 두번째 호출에서의 q값!!
그래서 a//b * v를 해서 두번째 호출에서의 나머지를 구함!!!
그리고 마지막으로 나온 a값이 gcd값이 되는것..
잘 이해가 되도록 먼저 p = 10, q = 15 로 한 과정을 손으로 써봤습니당
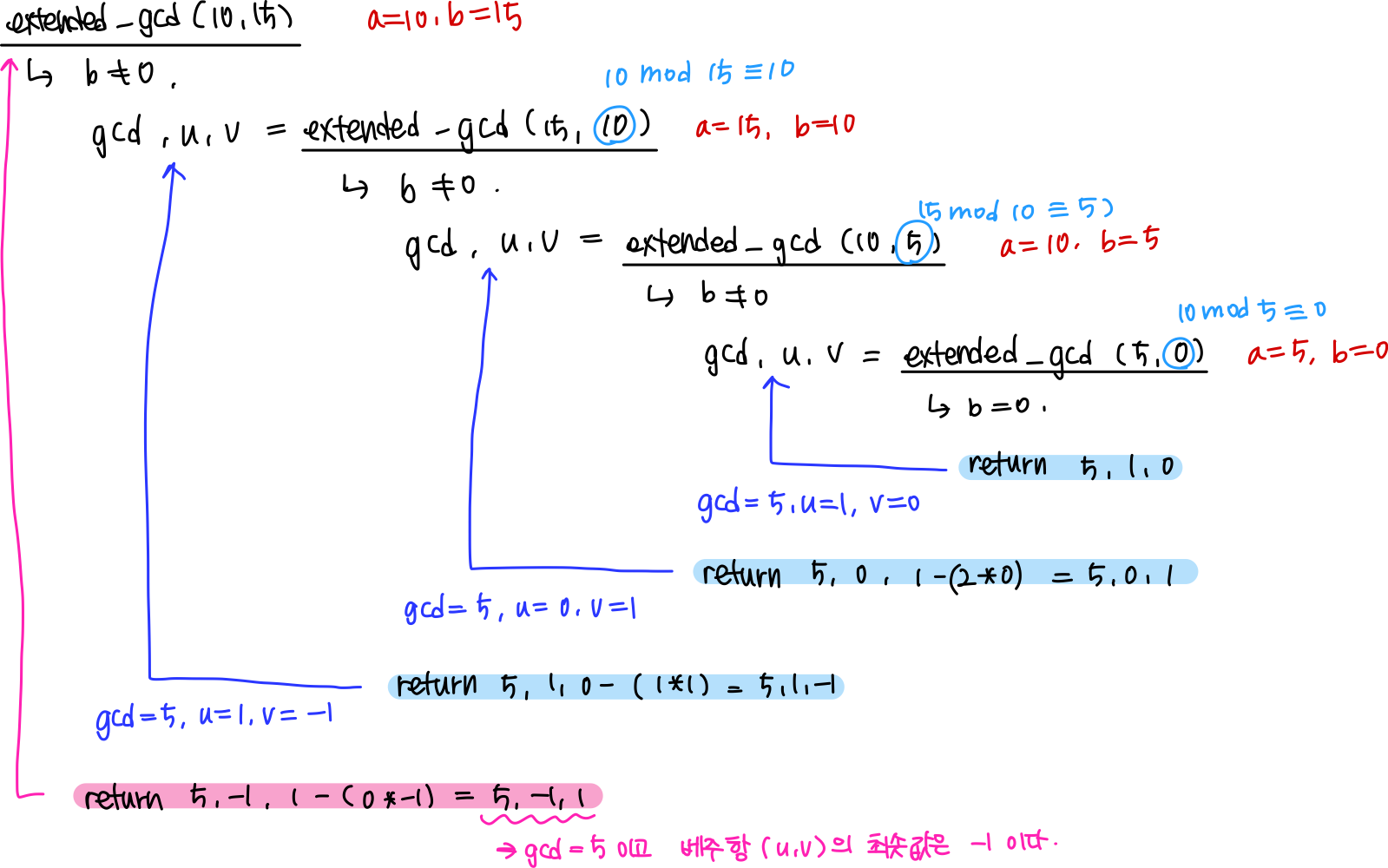
이해 완~
그럼 이제 퀴즈의 답은 뭘까요?
굳~
'WARGAME > cryptography' 카테고리의 다른 글
| [CryptoHack] Modular Arithmetic 2 (0) | 2024.01.16 |
|---|---|
| [CryptoHack] Modular Arithmetic 1 (0) | 2024.01.16 |
| [CryptoHack] Greatest Common Divisor (1) | 2024.01.03 |
| [CryptoHack] You either know, XOR you don't (0) | 2024.01.02 |
| [CryptoHack] Favourite byte (0) | 2024.01.02 |